1. 정보 (information)란?
확률 : 가능한 모든 상황에서 어떤 이벤트가 발생하는 빈도수
예를 들어 만일 99개의 파란종이와 1개의 빨간종이가 있다고 가정해보자. 만일, 파란종이가 나오면 놀라지 않을 것이고 빨간종이가 나오면 놀랄 것이다. 파란 종이가 나올 확률은 0.99로 높고, 빨간 종이가 나올 확률을 0.01로 낮기 때문이다.
즉 확률이높으면 그 사건이 발생해도 그 사건이 발생해도 놀라지 않고, 확률이 낮으면 그 사건이 발생했을 때 놀라게 된다.
확률과 놀람은 서로 반비례의 개념이다. 그래서 놀람을 수학적으로 표현하자면, 확률을 p(x)라고 할경우 놀람은 확률의 역수인, 1 / p(x)로 표현할 수 있다.
실제 정보이론에서 표현하는 놀람의 공식은 log(1/p(x)) 이다. 따라서 정보이론에서 정보량이란, 일종의 의외성(놀람)을 객관적인 수치로 표현한 것을 말한다.
log(1 / p(x)) = log 1 - log(p(x)) = 0 - log(p(x)) = - log(p(x))
정보이론에서 '놀람'이라는 표현보다는 보다 객관적인 지표의 의미가 있는 '정보'라는 단어를 사용한다.
(통계학에서는 놀랄만한 내용일 수록 정보량이 많다고 얘기하는 것이다) 확률의 반비례하는 것 정도는 기억해놓는 것이 좋다.
이때 로그의 밑은 응용분야에 따라 다르게 쓰일 수 있다고 한다. 대게 2, e, 10 중 하나를 사용할 수 있다. (각각을 사용했을 때 정보량의 단위는 bit, nit , dit 이다)
😯 그렇다면 정보량을 정의할 때 왜 굳이 log를 붙여서 정의했을까?
- 확률값(혹은 확률밀도 값)에 반비례하기 때문이다.
- 두 사건의 정보량을 합치면 각 사건의 정보량을 합친 것과 같아야하기 때문이다.
- 두 사건이 연달아 일어난다고 하면 얻게 되는 정보량은 첫번째 사건과 두번째 사건에 대한 정보량을 합한것으로 생각하는 것이 자연스러운데, 통계적으로 두 사건이 연달아 일어나면 확률의 곱으로 계산하게 되므로 log를 이용하여 정보량을 정의하면 각 사건이 연달아 일어나게 되었을 때 정보량은 합쳐지는 효과를 보이게 되는 것이다.
2. 엔트로피 : 평균 정보
물리학에서 무질서도라는 개념으로 사용된 Entropy는 확률통계학에서 확률분포의 불확실성을 나타내는 척도이다.
확률 분포에 대한 정보량의 기댓값으로 표현한다. ⇒ 놀람의 예상값(기댓값)
- 정보량이 많을수록 Entropy 값은 높아지며, 정보량이 적을수록 Entropy 값은 낮아진다.
- ( 엔트로피가 크다 = 무질서도가 크다 = 예측 불가능하다)
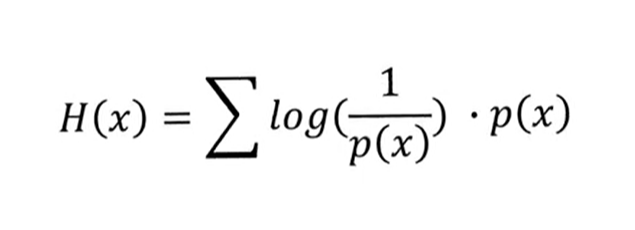
쉽게 예를 들어 동전과 주사위를 통해 Entropy를 계산해보자. 동전의 경우 확률이 1/2인 이산확률분포이며 주사위의 경우 확률이 1/6인 이산확률분포이다. 동전과 주사위를 던지는 상황에 대한 entropy는 각각 다음과 같이 계산된다.

위 예시를 통해 확률변수가 다양하게 나올 수 있는 경우, 즉 확률에 대한 불확실성이 큰 경우 Entropy가 더 크다는 것이다.
3. 크로스 엔트로피(Cross Entropy)
CE는 Q라는 모델의 결과에 대해 P라는 이상적인 값을 기대했을 때 우리게 얻게 되는 '놀라움'에 대한 값을 정보량으로 표현한 것이라는 점이다.타겟값과 모델의 출력값이 얼마나 다른지 표현한 식이며, 쉽게 말하자면 예측과 달라서 생기는 놀람도(정보량)이라고 할 수 있다.

예를 들어서 주사위를 굴린다고 해보자
| X | 1 | 2 | 3 | 4 | 5 | 6 |
| P(x = X) | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
| Q(x =X) | 1/2 | 1/10 | 1/10 | 1/10 | 1/10 | 1/10 |
이상적인 주사위와 다르게 우리가 실제로 주사위를 굴렸을 때, 우리가 얻게되는 놀라움의 정도를 계산해보면 다음과 같다.

즉, 이상적으로 생각하고 있는 주사위를 기대하고 실제로 굴려본 주사위의 실제값을 이용해 cross entropy를 계산하면 다음과 같다.

놀라움의 정도(이상과 현실과의 차이에 대한 놀라움)이 더 크다고 할 수 있다.
Q. 크로스엔트로피가 MSE보다 좋은 이유
MSE보다 손실을 더 잘 보여주기 때문이다. (특히 분류문제의 경우)

실제값이 1이라고 할 때, 예측값이 1에 가까울 수록 신경망의 예측력이 좋다고 볼 수 있다. 크로스 엔트로피의 손실값이 MSE보다 높고, 기울기도 훨씬 커서 예측값이 실제값이 멀면 멀수록 크로스 엔트로피가 MSE에 비해 효율적으로 손실을 최소화 할 수 있다.
4. KL Divergence : 정보 엔트로피의 상대적 비교
두 확률분포의 차이를 계산하는데 사용하는 함수로, 이상적인 분포에 대해 그 분포를 근사하는 다른 분포를 사용해 샘플링을 한다면 발생할 수 있는 정보 엔트로피를 계산한다. (P분포를 추정하는데 Q분포가 얼마나 적합한지로 해석 가능)

두 분포 사이의 차이에서 기존 분포 자체의 불확실성을 제거함으로써 두 분포가 얼마나 서로 다른 정보를 가지고 있는지 측정하는 개념이다. 즉, 두 분포가 유사할 경우 KL Divergence의 값은 0에 수렴하게 된다.
+ KL Divergence VS Cross Entropy
KL Divergence와 Cross Entropy는 유사하지만, KL Divergence는 두 확률 분포 간의 차이를 측정할 때 비대칭성을 가진다. KL Divergence에서 P와 Q가 바뀌면 결과가 바뀔 수 있지만, Cross Entropy는 항상 대칭적이다. 따라서 KL Divergence는 Cross Entropy보다 더 엄격한 지표로써 예측 모델의 성능을 더욱 정확하게 평가할 수 있다.
✍🏻 참고자료
https://www.youtube.com/watch?v=vAaReyHMfY8
https://angeloyeo.github.io/2020/10/26/information_entropy.html
https://roytravel.tistory.com/359
'STUDY > ML&DL' 카테고리의 다른 글
| [DL] Dropout (0) | 2024.06.20 |
|---|---|
| [DL] Data Augmentation (1) | 2024.06.20 |
| [DL] Batch Normalization (1) | 2024.06.19 |
| [DL] Activation Function , Non-linear Function (0) | 2024.06.18 |
| [CV] Diffusion이란? (1) | 2024.04.26 |
