활성화 함수의 특징 - 비선형함수(Non-linear Function)
< 간단히 말하자면 >
실제 세계의 많은 문제들은 변수 간의 복잡한 상호작용과 비선형 관계를 포함하고 있습니다. 예를 들어, 이미지 문제에서 픽셀 간의 관계는 단순한 선형조합으로는 표현하기 어려운데, 선형함수는 입력 변수의 선형조합으로 출력을 계산하기에 비선형적인 관계를 표현하는데는 한계가 있습니다. 반면 비선형함수는 입력값에 따라 출력이 비선형적으로 변화하므로 신경망이 복잡한 비선형 패턴을 학습할 수 있게끔 도와줍니다.
활성화 함수의 특징은 선형함수가 아닌 비선형함수여야 합니다. 선형함수란 출력이 입력의 상수배만큼 변하는 함수를 선형함수라고 하는데, 예를 들면 $ f(x) = Wx+b $ 라는 함수가 있을 때 W와b는 상수입니다. 이 식은 그래프로 그리면 직선으로 그려지며, 반대로 비선형 함수는 직선 1개로는 그릴 수 없는 함수를 의미합니다.
인공신경망의 성능을 높이기 위해서는 은닉층을 계속해서 쌓아야하는데, 활성화함수로 선형함수를 사용하게 되면 은닉층을 쌓을 수 없습니다. $ f(x) = Wx $로 가정한다면, 여기다가 은닉층을 2개 추가하여 출력층을 포함해서 $ y(x) = f(f(f(x))) $ 가 됩니다. 이를 식으로 표현하면 $ W*W*W*x$ 이고 이는 곧 $ W^3 = k $라고 정의해버리면 $ y(x) = kx $와 같이 표현이 가능합니다. 선형함수로는 은닉층을 여러번 추가하더라도 1회 추가한 것과 차이를 줄 수 없게 됩니다.
이러한 특성은 심층 신경망을 사용하는 이점을 상쇄시킵니다. 비선형 함수를 도입함으로써 각 층은 이전층의 출력에 비선형변환을 적용하여 새로운 표현을 학습할 수 있습니다. 이를 통해 신경망은 층이 깊어질 수록 점진적으로 추상화된 특징을 학습할 수 있으며, 이는 복잡한 문제를 해결하는데 필수적입니다.
✍🏻참고자료
1. Sigmoid function (시그모이드 함수)
$$ \sigma(x) = \frac{e^x}{e^x +1} = \frac{1}{1+e^{-x}} $$


🤔 sigmoid의 문제점
1. saturated neurons 'kill' the gradients
x가 무한대로 향해 갈수록 sigmoid 함수값이 0또는 1에 매우 가까워져 전체적으로 x축에 평행한 모습을 보입니다. 이를 saturated하다 라고 표현하는데 이런 경우에는 backprop를 할 때 치명적인 문제가 생깁니다.

위의 그림을 볼 때 x의 절대값이 커질수록 gradient의 값은 모두 0이 됩니다. 그렇게 되면 backprop 진행 시 모두 0이 곱해지는 결과를 야기하게 됩니다 (gradient vanishing). 즉 학습이 더 이상 진행되지 않는 것입니다.
2. sigmoid outputs are not zero-centerd
Zero-centerd란? 그래프의 중심이 0인 형태로 함수값이 양수 혹은 음수에만 치우치지 않고 실수 전체에서 나타나는 형태를 의미합니다. sigmoid는 위의 그래프에서도 알 수 있듯이 함수값이 항상 0보다 크거나 같은 형태를 나타내는데 이러한 경우에 문제점을 생각해봅시다.
해당 부분을 이해하는데 조금 어려웠습니다.. 많은 자료를 참고해서 이해한대로 작성해본 것입니다.

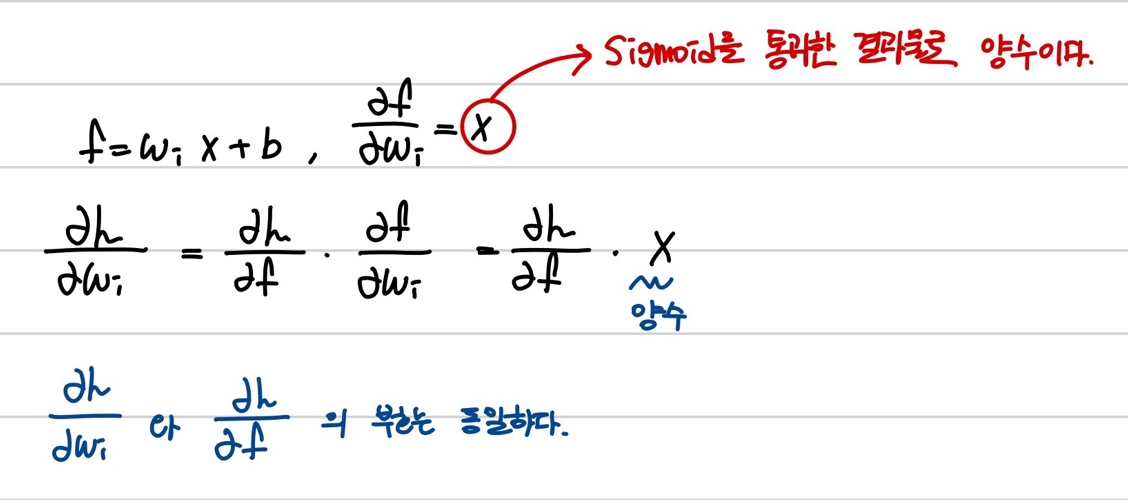
이는 가중치 업데이트가 항상 같은 방향으로만 이루어짐을 의미합니다.
x가 항상 positive라고 가정했을 때, W의 gradient 는 항상 positive 또는 Negative 입니다. 2차원의 W값이 있다고 가정하고, x축을 w1 , y축을 w2로 가정해봅시다. 이때 W의 update는 W1이 증가했을 때 W2도 증가하는 경우, W1이 감소했을 때 W2도 감소하는 경우 2가지로 update됩니다.
그런데 최적의 해가 W1가 증가할 때 W2가 감소하는 방향입니다. (위의 그래프에서 파란색 직선)
W의 gradient가 항상 Positive or Negative일 경우 비효율적으로 최적해를 탐색하게 됩니다. 파란색 직선으로 해를 탐색하는 것이 아닌 'zig-zag' 로 해를 탐색하게 되는 것입니다. 여러번 탐색해야하기 때문에 비효율적인 weight update방법이 됩니다.
이것이 바로 일반적으로 zero-mean data를 원하는 이유입니다. 입력 x가 양수와 음수를 모두 가지고 있으면 gradient w가 모두 positive or negative 방향으로 움직이는 것을 막을 수 있습니다.
3. exp() 연산의 비용은 크다.
2. Tanh
- 출력값을 -1에서 1사이로 변환시켜줍니다.
- zero-centered 합니다.( sigmoid의 문제점을 해결해줍니다.)
- 다만, 여전히 포화된 입력값에선 Gradient가 소실된다는 단점이 있습니다.
3. ReLU
ReLU는 x가 양수인 지점에 한해서 saturate 문제에서 많이 벗어난다(포화되지 않음) .또한 ,단순히 max함수를 이용하기 때문에 계산이 매우 빠르다는 장점이 있습니다.

이 ReLU 함수는 Sigmoid / Tanh 보다 실질적으로 빨리 수렴합니다. (대략 6배 이상 빠르다고 합니다. 😯)
하지만 여전히 해당 함수 output 모두 양수이기에 zero-centered 하지 못하다는 단점이 있습니다. x가 음수인 지점에서는 saturated 하기에 학습시 gradient가 없어지게 되는 문제가 있습니다.
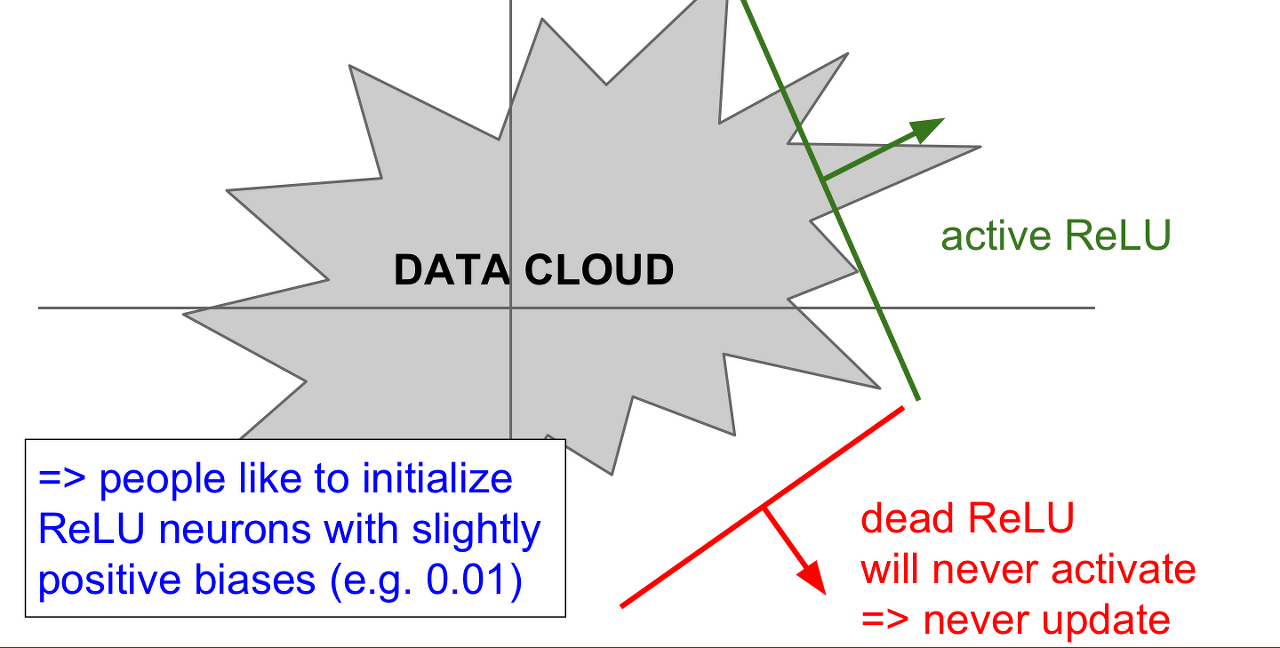
또한, ReLU가 data cloud로 부터 떨어져 있을 때 DeadReLU가 발생할 수 있습니다. 가중치 평면에 data cloud에서 멀리 떨어져 있는 경우, 어떤 입력데이터에서도 activate 되지 않습니다. 더 흔한 경우는 learning rate가 높은 경우입니다. 가중치 파라미터 업데이트의 learning rate가 높은 경우 ReLU가 데이터의 mainfold를 벗어나게 됩니다. 이렇게 되면 활성화되지 않고 업데이트가 진행되지 않습니다. 즉, 죽어버리게 됩니다...🥹 이런일들은 학습과정에서 흔하고 충분히 발생할 수 있다고 합니다. 따라서 ReLU를 사용할때는 learning rate를 작은 값으로 초기화 해야합니다.
4. LeakyReLU
ReLU 이후 보완된 함수 중 하나가 Reaky ReLU입니다.

- ReLU와 유사하지만 음의 영역에서 더 이상 0이 아닙니다.
- 즉, 모든영역에서 saturated 되지 않습니다.
- 여전히 계산이 효율적이고 빠릅니다.
- 더 이상 Dead ReLU 현상이 없게됩니다.
5. GELU(Gaussian Error Linear Unit)
GeLU의 저자들은 Dropout + zoneout+ ReLU를 조합하여 쓰는 것에 영감을 받아서 개발한 activation function이라고 합니다. RNN 계열에서 사용되는 zoneout을 배제하고, dropout + ReLU에 대해서만 생각을 해보겠습니다. ReLU는 0이하는 버리고 0이상의 값들은 그대로 input 으로 가져가는 역할을 합니다. Dropout은 0부터 1까지 일정확률로 마스킹을 해주는 역할을 합니다.


이 과정을 베르누이 분포의 함수(dropout의 대체) 와 input x (ReLU)의 곱으로 표현한 것이 바로 GELU라고 할 수 있습니다. 베르누이 분포는 정규분포 함수의 누적분포함수를 생각하면 됩니다. 대다수의 실험에서 GELU는 평균 0 그리고 분산 1로 정의하여 사용하며, 성능 또한 괜찮은 것으로 알려져있습니다.
- ReLU와 유사하면서도 조금 더 smoothing한 형태입니다.
- 0이하의 값에서도 작게나마 gradient를 전달한다는 장점을 지니고 있습니다.
- 여기서 개인적으로 궁금한 점은 GELU도 음의 무한대 값이 input으로 들어올 경우 미분값이 0이 되어 gradient가 소실되는 문제가 발생할 듯한데, 어떻게 BERT, Vit 등 최신 모델에서 좋은 성능을 보이고 있는건지 궁금하네요.
✍🏻참고자료
https://arxiv.org/pdf/1606.08415
https://techmoong.medium.com/gaussian-error-linear-units-gelus-58503f1ac7c7
'STUDY > ML&DL' 카테고리의 다른 글
| [DL] Dropout (0) | 2024.06.20 |
|---|---|
| [DL] Data Augmentation (1) | 2024.06.20 |
| [DL] Batch Normalization (1) | 2024.06.19 |
| [DL] CrossEntropy , KL Divergence (0) | 2024.06.14 |
| [CV] Diffusion이란? (1) | 2024.04.26 |
